מבוא
מחלק מתח הוא מעגל פשוט שהופך מתח גבוה למתח נמוך יותר. עם רק שני נגדים בטור ומתח כניסה, נוכל לקבל ביציאה מתח שהוא חלק מהכניסה. מחלקי מתח הם אחד המעגלים הבסיסיים ביותר באלקטרוניקה. אם ללמוד על חוק אוהם היה דומה ללימוד ה-א'-ב', אז ללמוד על מחלקי מתח זה כמו ללמוד לאיית "חתול".אלה דוגמאות של פוטנציומטרים, נגדים משתנים שיכולים לייצר מחלק מתח מתכוונן. נרחיב עליהם בהמשך.
מדריך זה מכסה
- איך נראה מעגל מחלק מתח
- איך מתח היציאה תלוי במתח הכניסה ונגדי החלוקה
- איך מחלקי מתח מתנהגים בעולם האמיתי
- יישומי מחלקי המתח מהחיים האמיתיים
מדריכים מומלצים:
מדריך זה מבוסס על ידע בסיסי באלקטרוניקה. אם עדיין לא עשיתם זאת, אנו ממליצים על קריאת מדריכים הבאים:- מהו מעגל?
- מעגלים טוריים ומקביליים
- מתח, זרם, התנגדות וחוק אוהם
- איך משתמשים ברב-מודד
- איך משתמשים במטריצה
- Analog-to-Digital Conversion - TODO
מחלק מתח אידיאלי
ישנם שני חלקים חשובים במחלקי מתח: המעגל והמשוואה.המעגל
מחלק מתח מתקיים כשמספקים מתח על פני שני נגדים המחוברים בטור. אתם יכולים לראות את זה מצוייר בכמה דרכים שונות, אבל כולם למעשה יהיו אותו המעגל: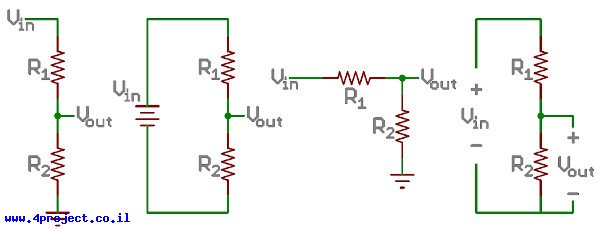
נקרא לנגד הקרוב למתח הכניסה (Vin) כ-R1, והנגד שקרוב יותר לאדמה כ-R2. המתח שנופל על R2 נקרא Vout, זהו המתח המחולק שהמעגל שלנו נועד לייצר.
זה כל מה שיש במעגל! Vout הוא המתח המחולק שבסופו של דבר יהיה חלק ממתח הכניסה.
המשוואה
הנוסחה של מחלק המתח מניחה שאתם יודעים 3 ערכים של המעגל: מתח הכניסה Vin וערכי שני נגדים R1 ו-R2. בהינתן ערכים אלה, נוכל להשתמש בנוסחה הבאה כדי למצוא את ה-Vout:
הנוסחה אומרת שמתח היציאה יהיה ביחס ישר למתח הכניסה וליחס בין R1 ו-R2. נחזק את זה בתרגילים בהמשך המדריך. אבל בינתיים תרשמו ותזכרו את הנוסחה.
הפשטות
יש כמה הכללות שכדאי לזכור כשמשתמשים במחלקי מתח. אלה ההפשטות שגורמות לחישוב ערכי מעגל מחלק מתח לקצת יותר קלים.
אם R1 שווה ל-R2, מתח היציאה יהיה חצי ממתח הכניסה. זה נכון בלי קשר לערכי הנגדים.
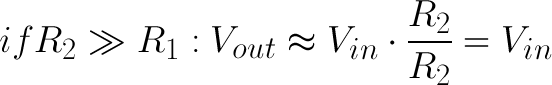
אם R2 הרבה יותר גדול (בסדרי גודל) מ-R1, מתח היציאה יהיה קרוב מאוד למתח הכניסה. מפל המתח על R1 יהיה מאוד קטן.

לעומת זאת, אם R2 יהיה הרבה יותר קטן מ-R1, מתח היציאה יהיה פיצי בהשוואה לכניסה. רוב מתח הכניסה יהיה על R1.
יישומים
למחלק מתח יש המון יישומים, הוא בין המעגלים הנפוצים ביותר בקרב מהנדסי אלקטרוניקה. הנה רק כמה מהמקומות הרבים בהם תמצאו מחלק מתח.פוטנציומטרים
פוטנציומטר הוא נגד משתנה שאפשר להשתמש בו כדי לייצר מחלק מתח מתכוונן.אוסף של פוטנציומטרים שונים. משמאל למעלה בכיוון השעון: פוטנציומטר סטנדרטי של 10K, ג'ויסטיק שני צירים, חיישן כוח, זחלן, קלאסי בזווית, ופוטנציומטר של 10K שמתאים למטריצה.

בתוך הפוטנציומטר יש נגד אחד ו"מגב", שנע על הנגד ומחלק אותו לשניים כאשר התזוזה תשנה את היחס בין שני החלקים. מבחוץ יהיו בדרך כלל 3 חיבורים, שניים מחוברים לקצוות של הנגד, והשלישי למגב של הפוטנציומטר.
סמל של הפוטנציומטר. פינים 1 ו-3 אלה קצוות הנגד. פין 2 מחובר למגב/זחלן:

אם הפינים החיצוניים יחוברו למקור מתח (אחד לאדמה והשני ל-Vin), מתח היציאה (Vout בפין האמצעי) יחכה מחלק מתח. סובבו את הפוטנציומטר לכיוון אחד והיציאה תהיה אפס, סובבו לכיוון השני והיציאה תתקרב למתח הכניסה. כשהמגב/זחלן במצב האמצעי, מתח היציאה יהיה חצי של מתח הכניסה.
פוטנציומטרים מגיעים במגוון צורות שונות ויש להם הרבה יישומים משלהם. הם יכולים לשמש ליצירת מתח ייחוס, לכוון תחנת רדיו, למדוד מיקום הג'ויסטיק, או המון יישומים אחרים שדורשים מתח כניסה משתנה.
קריאת חיישנים התנגדותיים
הרבה חיישנים בעולם האמיתי הם רכיבים התנגדותיים פשוטים. חיישן אור (photocell) הוא נגד משתנה, שמייצר התנגדות פרופורציונלית לכמות האור שהוא רואה. רכיבים אחרים כמו חיישני קיפול, חיישני לחץ, וגם תרמיסטורים (חיישני טמפרטורה), גם הם נגדים משתנים.מסתבר שלמיקרו-בקרים די קל למדוד מתח (לפחות לאלה עם מעגלי המרה אנלוגי לדיגיטלי (TODO), הנקראים גם ADC). למדוד התנגדות? לא כל כך קל. אבל, אם מוסיפים נגד לחיישן התנגדותי, נוכל לייצר מחלק מתח. ברגע שידוע לנו מתח היציאה של מחלק המתח, נוכל לחזור ולחשב את ההתנגדות של החיישן.
לדוגמה, התנגדות של חיישן אור משתנה בין 1kΩ באור ובערך 10kΩ בחושך. אם נשלב את זה עם נגד קבוע של ערך איפה שהוא באמצע, נניח 5.6kΩ, נוכל לקבל טווח מתחים רחב מתוך מחלק המתח שניצור.
חיישן האור הוא חצי ממחלק המתח הזה. מודדים את המתח כדי למצוא את התנגדות החיישן:

אור מלא
- R1 קבוע בערך של 5.6kΩ
- R2=1kΩ
- יחס בין הנגדים R2/(R1+R2) שווה ל: 0.15
- מתח Vout = 0.76V
אור חלקי
- R1 קבוע בערך של 5.6kΩ
- R2=7kΩ
- יחס בין הנגדים R2/(R1+R2) שווה ל: 0.56
- מתח Vout = 2.78V
חושך
- R1 קבוע בערך של 5.6kΩ
- R2=10kΩ
- יחס בין הנגדים R2/(R1+R2) שווה ל: 0.67
- מתח Vout = 3.21V
שינויי מתח של כ-2.45V בין חושך לאור. רזולוציה יפה לרוב מעגלי ADC.
המרת רמות לוגיות
חיישנים מתקדמים יותר יכולים לשדר את הקריאות שלהם דרך ממשקים משוכללים כמו UART, SPI או I2C (TODO). רוב החיישנים האלה פועלים במתחים יחסית נמוכים כדי לחסוך בחשמל. ובכל זאת, זה לא חריג לראות את חיישני מתחים הנמוכים האלה מתממשקים עם מיקרו-בקרים הפועלים במתחים גבוהים יותר. זה מוביל לבעיית המרה של רמות לוגיות, שיש לה מספר פתרונות, כולל מחלק מתח.לדוגמה, חיישן תאוצה ADXL345 תומך במתח מקסימלי של 3.3V, כך שאם תרצו לחבר אותו לכרטיס Arduino (בהנחה שהוא עובד ב-5V), תצטרכו לעשות משהו כדי להוריד את המתח של קווי התקשורת מ-5V ל-3.3V. מחלק מתח! כל מה שצריך זה כמה נגדים שהיחס שלהם יחלק את ה-5V לבערך 3.3V. בדרך כלל לצרכים אלה רצוי להשתמש בנגדים בערכים של 1kΩ-10kΩ. בואו נעשה כך:

נגדים של 3.3kΩ (כתום-כתום-אדום) הם ה-R2. נגדים של 1.8kΩ הם ה-R1. זוהי דוגמה של מחלק מתח על מטריצה שמוריד את מתח הקווים של 5V ל-3.24V.
זכרו שפתרון זה טוב רק לכיוון אחד. מחלק מתח לא יעזור לכם לעלות ממתח נמוך למתח גבוה אם יש בכך צורך.
מה אסור לעשות
עד כמה שזה מפתה להשתמש במחלק מתח כדי להוריד אותו, נגיד, מספק כוח של 12V ל-5V, לא משתמשים במחלק מתח כדי לספק מתח לעומס.כל הזרם שהעומס צורך יצטרך לעבור דרך הנגד R1. הזרם והמתח שנופל על R1 מייצרים הספק שמפוזר ממנו בצורה של חום. אם ההספק הזה גבוה מההגדרות של הנגד (בדרך כלל בין 1/8W ל-1W), החום מתחיל להיות בעיה רצינית, שעלול להמיס את הנגד.
כל זה בלי להזכיר עד כמה אספקת מתח דרך מחלק מתח תהיה לא יעילה. בכללי, אל תשתמשו במחלק מתח לאספקת מתח לשום דבר, גם אם דרוש הספק מאוד קטן. אם אתם צריכים להוריד מתח כדי להשתמש בו כספק כוח, השתמשו במייצבי מתח או ספקים ממותגים.
נקודות בונוס: ההוכחה
אם מחלקי המתח עדיין לא הספיקו לכם, בסעיף זה נראה איך משתמשים בחוק אוהם כדי להגיע לנוסחה של מחלק המתח. זהו תרגיל מהנה, אבל לא סופר חשוב כדי להבין מה מחלק מתח עושה. אם זה מעניין אתכם, תתכוננו להנות עם חוק אוהם ואלגברה.הערכת מעגל
אז אתם רוצים למדוד את המתח ב-Vout? איך משתמשים בחוק אוהם כדי לייצר את הנוסחה של המתח בנקודה זו? בואו נניח שאנחנו יודעים את הערכים של Vin, R1 ו-R2, אז נייצר את הנוסחה של Vout בהתבסס על ערכים אלה.בואו נתחיל בציור של הזרמים במעגל, I1 ו-I2 יציינו את הזרם שעובר דרך הנגדים המתאימים.

המטרה שלנו היא לחשב את Vout. מה אם נפעיל את חוק אוהם על המתח הזה? זה די קל, כי יש לנו רק נגד אחד וזרם אחד שמעורב:

נהדר! אנחנו יודעים את ערך ה-R2, אבל מה לגבי I2? זהו ערך לא ידוע, אבל אנחנו כן יודעים עליו משהו בכל זאת. נוכל להניח (וזו הנחה מאוד גדולה) ש-I1 שווה ל-I2. אוקי, האם זה עוזר לנו? חכו עם זה רגע. המעגל שלנו נראה עכשיו כך, כאשר I שווה ל-I1 וגם ל-I2.

מה ידוע לנו על Vin? זהו מתח על שני הנגדים R1 ו-R2. הנגדים מחוברים בטור, כך שהערכים שלהם מתחברים, כך שאפשר לומר ש:

ולרגע נוכל לפשט את המעגל לזה:

זהו הבסיס של חוק אוהם! Vin שווה ל- I * R. כך שאם נחזיר את R להיות R1+R2, נוכל לכתוב את זה כך:

ומכוון ש-I שווה ל-I2, נציב את זה בנוסחה של Vout ונקבל:

וזוהי הנוסחה של מחלק מתח! מתח היציאה הוא חלק ממתח הכניסה, והחלק הזה הוא R2 מחולק בסכום של R1 ו-R2.
לאן ממשיכים?
עכשיו כשאתם מבינים את העיקרון של אחד המעגלים הנפוצים באלקטרוניקה, יש עוד עולם שלם של דברים חדשים ללמוד!רוצים ללמוד איך מיקרו-בקר כמו ה-Arduino יכול לקרוא מתחים אנלוגיים שמיוצרים ע"י מחלק מתח?
- Analog-to-Digital Converters - TODO
עם הכוח של מחלק מתח ו-ADC תוכלו להשיג הרבה בעולם האלקטרוניקה. בדקו גם את המדריכים הבאים:
- בחלק מהדגמים של חיישני תאוצה (TODO) וג'רוסקופים (TODO) יש יציאות אנלוגיות שכדי לקבל ערכים שימושיים מהם צריך להשתמש ב-ADC.
- Pulse Width Modulation (PWM) - TODO זה כמו יציאה אנלוגית, ההפך מהכניסה האנלוגית.
- ה-INA169 (TODO) מאפשר למדוד זרם ע"י שימוש ב-ADC.
- ע"י שימוש במחלק מתח ו-ADC תוכלו לקרוא ערכים של הרבה חיישנים ורכיבים כמו נגדים משתנים, ג'ויסטיקים, זחלנים וחיישני לחיצה, שהם רק חלק מהרבה מאוד רכיבים אחרים.
- פונקציית ()map של Arduino.
- קווי ה-Analog של Arduino.